之前都在介紹函式，今天休息一下先不施放咒語，來認識認識歐拉常數吧！

數學課

數學中有一個跟π一樣，是個很特別的常數—「e」，他叫Euler's number歐拉常數，或稱自然常數。

我們知道π是一個圓的圓周長跟直徑的比例，那e是在算什麼呢？

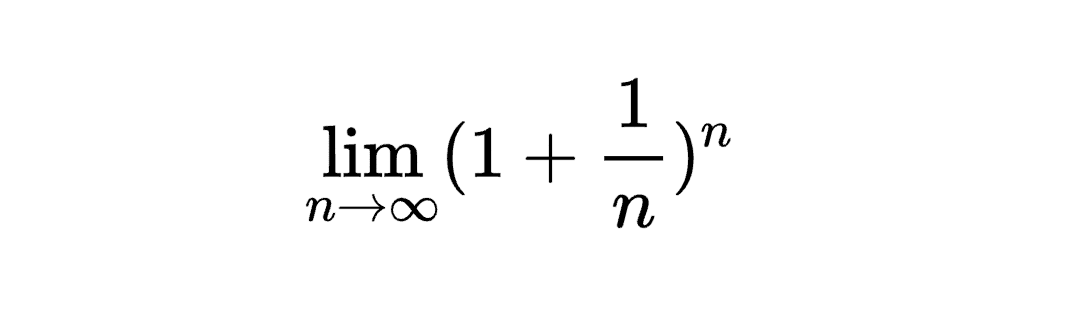
e是從前數學家嘗試計算的一個常數，他嘗試計算的內容就是(1 + 1/n)的n次方，而將這個n取極限值到無限大，他會趨近於一個數，這個數就是e，他會趨近於2.7182818......，總之就是2.7多，是一個無限不循環小數、無理數。

那為什麼他們要計算這個東西呢？

「不要問，你會怕。」

不怕是嗎？那稍微提一下。

歷史

16世紀末～17世紀初時的蘇格蘭數學家約翰·納皮爾（John Napier）
他製作了一個對數表，目的是為了簡化當時學術界針對許多巨大數相乘的計算，而在製作對數表，透過查對數表就能將大數的乘法化簡成較小數的加法，但這時候停在了指數概念的階段，當時他並沒有將這個數字記錄下來。

後來雅各布·伯奴利（Jacob Bernoulli）
他探討了複利問題而算出了自然常數的值。

直到最後歐拉利用了前面的對數概念結合複利計算的概念，將這個數做了完整的整理及應用，這才廣泛被人理解，所以通常人們會稱這個數被稱為「歐拉常數」。

當這個數被提出之後，因為他一些厲害的特性，在生物學、物理學、電學等領域都經常出現他的蹤影。

複利計算

假設今天有個銀行計算計算利息採用複利，一年分幾次利率就除以多少，如果一年算兩次，年利率就是50%，算給大家看：

假設你存100元，半年後就會計算利息變成100 * (1 + 1/2)，也就是150元，這時候本金就變成了150元，一年後計算第二次利息150 * (1 + 1/2)也可以理解成[100 * (1 + 1/2)] * (1 + 1/2)，也可以看成100 * (1 + 1/2)^2就變成了225元，如果一年分四期，就會是100 * (1 + 1/4)^4；那如果分無限多期呢？無時無刻都在領利息，但利息無限小，一年後你的錢就會變成原來的e倍，也就是2.718...倍。

自然常數的應用

這個數被提出後也被用在了「指數函數」、「以e為底的自然對數」，也被運用在許多數學公式上；生物學中，細胞分裂與人口成長常常會遵循指數成長的模式，而這個生長的速率與自然常數也有直接關係。

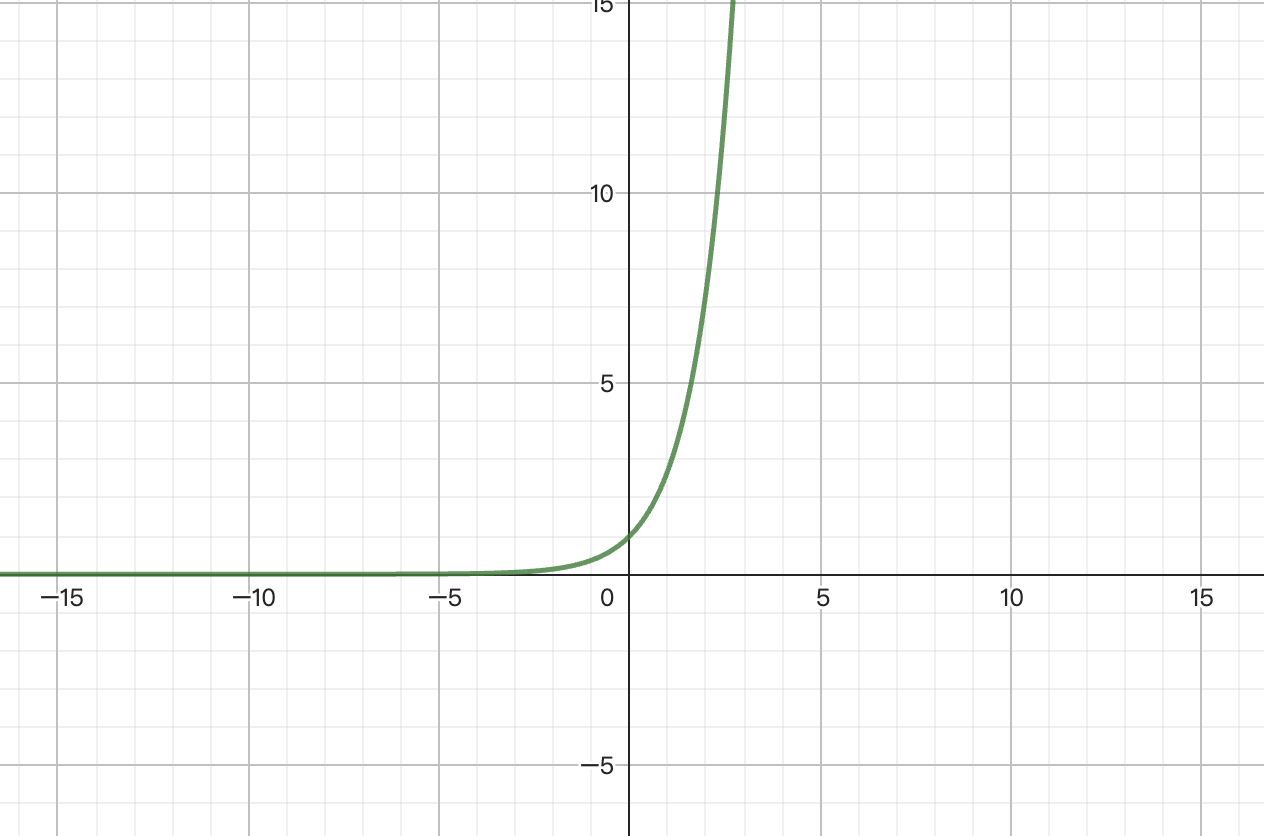
指數函數exp(x)圖形

可以想像我們剛剛在算複利的時候是以原來的本金計算第一期的利息，而計算第二期利息時就會以上次計算的結果作為本金，以此類推就有種利滾利的概念；而在生物繁衍的角度也是如此，這一代生出的下一代一樣會在生出他們的下一代，跟利滾利其實概念很類似，都是累積效應、指數成長的概念，這就是為什麼自然常數跟很多領域都有所相關。

而在指數函數中很有趣的一項特性便是在指數函數上的每個點取切線斜率（微分），恰恰好就會是這個點的值，這點特性就可以形容非常多的情況，所以才被廣泛運用在各個領域。

關於更多歐拉常數的應用可以進維基百科看看更深入的應用。

聽到這裡連我自己都不知道在說什麼了（開玩笑的我當然知道）

Math.E

介紹完歐拉常數，回到我們的Math.E，它代表的也就上剛剛介紹的歐拉常數，他大約是2.718。

規範

可以注意到描述器中幾個設定都是false，

• Writable不能被改寫
• Enumerable不能被尋訪
• Configurable設定不能被修改。

今天認識了歐拉常數，相信以後再看到e應該就不那麼害怕了吧！對吧？

參考資料：
維基百科-歐拉常數
MDN-Math.E
ECMAScript-Math.E
甚麼是e？